
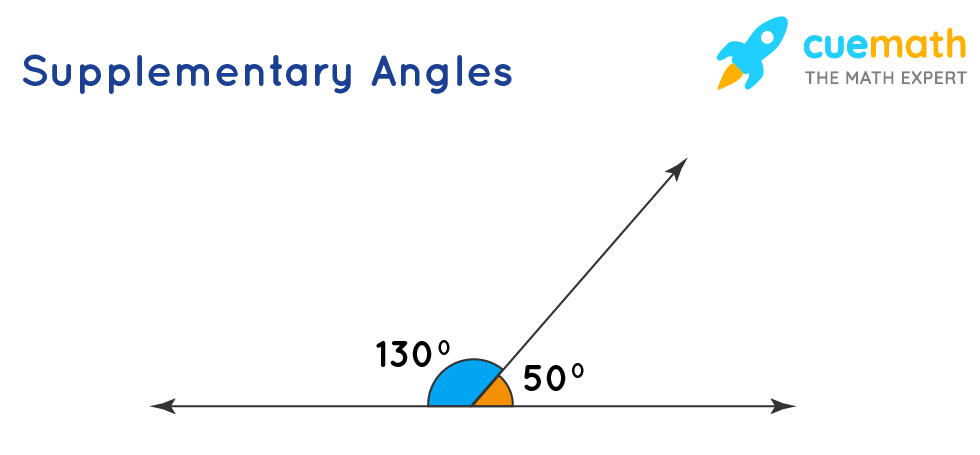
The complementary angles are the angles whose sum of values gives a right angle i.e. Generally, they are both opposite to each other. The difference between both complementary angles and supplementary angles can be observed in the above figure. The complementary angles and supplementary angles can be understood through the below figure. On joining all the two supplementary angles we will get a straight line. The pair of angles that forms supplementary angles whose values equal to 180° are called supplements to each other. The basis of all these angles is angle measurement. If the addition of two angles gives 90° then it is called complementary angles and if the values of the sum of two angles will be 180° then it is called supplementary angles. The identification of complementary and supplementary angles is done based on the addition of two angles. Complementary Angles and Supplementary Angles In the above figure angles, XYZ and ABC are complementary angles as their sum is equal to 90°. The non-adjacent complementary angles are shown in the figure below. It has no common arm and vertex but the sum of both angles should be 90° always. The pair of two complementary angles which are not adjacent to each other are called non-adjacent complementary angles. The figure is shown below in which angles AOC and BOC have the same arm and vertex which are adjacent complementary angles. The pair of angles having a common arm and vertex are called adjacent complementary angles. There are the following two types of complementary angles which are discussed in detail. The angles firms a pair of complementary angles are called complement to each other. Two Types of Complementary AnglesĪs we discussed when any two angles having their sum of values form a right angle are called complementary angles. The angles which form a pair of complementary angles are called complements to each other. In the above figure the angles AOC and BOC having values in order of 30°&60°, 40°&50°, 65°&25°, 48°&42°, and so on their sum will be 90°. It is a very essential criterion for complementary angles. Two angles are said to be complementary angles if their sum is equal to 90°. The values of both the angles form a right angle of 90°. The complementary angles are defined as the pair of two angles whose sum of values is equal to the 90°. You can see the complementary angles in the above figure in which two angles form a right angle. The angle whose sum of values is equal to 90° then the pair of angles are termed as complementary angles. If the values of the sum of two angles are equal to the right angle known by complementary angles.
The values of angles should be equal to the right angle of 90°. The complementary angles are identified by only the values of angles. Here the angles of AOC and BOC are complementary. The values of pair of angles followed by 60° and 30°, 40° and 50°, etc.

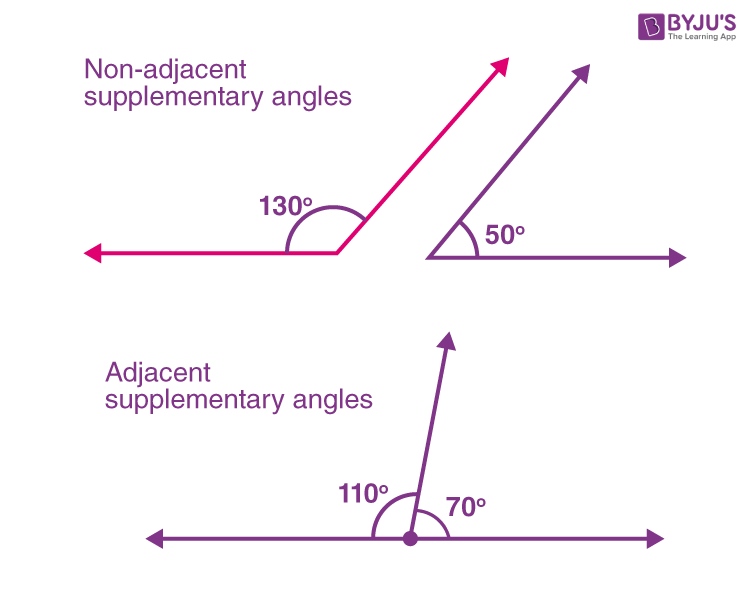
In geometry, if the sum of any two angles measures equal to the right angle and such pairs of angles are termed complementary angles. And both the angles are called complement each other. Complementary Angles and Supplementary AnglesĬomplementary Angles: When two angles are added and the sum of values is 90° called complementary angles.As discussed in the past, supplementary angles don’t have to form other angles. Let’s move on to the second pair of angles, $\angle ABC$ and $XYZ$. This is consistent with what was established about congruent supplementary angles. This means that the only time that a linear pair of angles (consequently, a pair of supplementary angles) are congruent to each other is when they are both right angles.
SUPPLEMENTARY ANGLES GEOMETRY DEFINITION HOW TO
Read more How to Find the Volume of the Composite Solid?


 0 kommentar(er)
0 kommentar(er)
